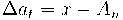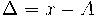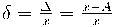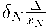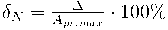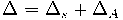Matavimo paklaidos

Matavimas – tai eksperimentinis fizikinio dydžio vertės nustatymas, naudojant technines matavimo priemones. Matavimai gali būti tiesioginiai ir netiesioginiai.

Tiesioginiai – tai tokie matavimai, kai ieškomąjį fizikinį dydį randame darydami bandymą. Tiesioginiai matavimai – tai temperatūros matavimas termometru, ilgio – liniuote, slėgio – barometru ir pan.

Netiesioginiai – kai nežinomąjį dydį randame matuodami ne jį patį, bet kitus dydžius, funkciškai susijusius su pirmuoju. Tarkim, greitį randame matuodami nueitą kelią ir laiką, varžą – srovę ir įtampą. Matavimo metu gaunamas matavimo rezultatas, t. y., matuojamojo fizikinio dydžio vertė. Ji išreiškiama tam tikru matavimo vienetų skaičiumi. Todėl matavimo rezultatas sudarytas iš skaičiaus ir matavimo vieneto.

Matavimo vienetas – fizikinis dydis, kurio vertė pagal susitarimą laikoma lygi vienetui.

Nepriklausomai nuo to, koks yra matavimo rezultatas, egzistuoja tikroji matuojamojo dydžio vertė. Matuodami galime rasti tik matuojamojo dydžio vertę, pakankamai artimą tikrajai, kurią konkrečiam matavimui galima naudoti vietoje tikrosios.

Matavimo vienetų visuma, sudaryta tam tikru įteisintu principu, vadinama matavimo vienetų sistema. Matavimo vienetų sistemai priklausantys vienetai skirstomi į pagrindinius, išvestinius ir papildomuosius. 1960 m. XI visuotinoji konferencija matų ir saikų klausimu nustatė vieningą tarptautinę vienetų sistemą (System Internacional), sutrumpintai žymimą SI. SI pagrindas yra septyni gerai apibrėžti pagrindiniai vienetai:

• metras (m),
• kilogramas (kg),
• sekundė (s),
• amperas (A),
• metras (m),
• kilogramas (kg),
• sekundė (s),
• amperas.

Papildomieji SI vienetai – tai plokščio ir erdvinio kampo vienetai: radianas (rad) ir steradianas (sr). Išvestiniai SI sistemos vienetai sudaromi iš pagrindinių ir papildomųjų.

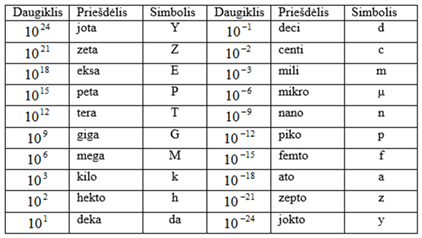
Kadangi matuojamųjų dydžių verčių ruožas yra labai platus, tai SI viene­tais naudotis ne visada patogu, todėl leidžiama naudotis kartotiniais ir daliniais vienetais. Šiems vienetams sudaryti vartojami daugikliai. Kartotinių ir dalinių vienetų pavadinimai turi daugiklius atitinkančius priešdėlius

Eksperimentiškai nustatant matuojamojo dydžio vertę, gaunamas dydis, kuris skiriasi nuo tikrosios matuojamojo dydžio vertės. Todėl matuojant visuomet turėsime paklaidą.

Matavimo paklaida - tai matuojamojo dydžio matavimo rezultato ir tikrosios matuojamojo dydžio vertės skirtumas:

$\Delta a_t =x-A_n$,

čia x – matavimo rezultatas, o A_n – tikroji matuojamojo dydžio vertė. Taip apibrėžta paklaida vadinama tikrąja matavimų paklaida. Ji praktiškai negali būti gaunama, nes tikroji matuojamojo dydžio vertė yra nežinoma. Praktikoje tenka tenkintis šios paklaidos įverčiu Δ, vietoje įrašius sutartinę matuojamojo dydžio vertę A:

$\Delta=x-A$.

Matavimų paklaidos atsiranda dėl matavimų metodų ir priemonių bei mūsų jutimo netobulumo. Tobulėjant matavimų metodams ir priemonėms, matavimų paklaidos mažėja ir matavimo rezultatas gaunamas artimesnis tikrajai matuojamojo dydžio reikšmei.

Skaičiuojant paklaidas pagal 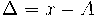$\Delta=x-A$, jos išreiškiamos matuojamojo fizikinio dydžio vienetais. Tokia paklaida vadinama absoliutine paklaida. Toks paklaidos išraiškos būdas nėra labai geras, nes jis neparodo, ar paklaida didelė, ar maža, lyginant ją su matuojamojo fizikinio dydžio verte (pvz.: ΔU = 0,5 V, kai x = 100 V – maža paklaida, tuo tarpu, kai x = 1 V, tokia paklaida yra gana didelė). Todėl praktikoje dažniau naudojamos santykinės paklaidos.

Santykinė paklaida – absoliutinės paklaidos ir matavimo rezultato santykis:

$\delta= \frac{ \Delta }{x} =\frac{ x-A}{x}$.

Ši paklaida dažnai išreiškiama procentais. Viso matavimo diapazono santykinė paklaida nėra pastovi, todėl įvedama redukuotoji (normuotoji) paklaida:

$\delta_N \frac{ \Delta }{x_N}$

čia x_N – normuojantis tos pačios rūšies dydis, su kuriuo lyginama paklaida. Tai gali būti, pvz., maksimali matuojamojo dydžio reikšmė.

Redukuota santykinė paklaida nusako elektrinio matavimo prietaiso tikslumo klasę.

$\delta_N= \frac{ \Delta }{A_{pr. max}} \cdot 100 \%$

Dažniausiai sutinkamos matavimo prietaisų tikslumo klasės:

0,02; 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Matavimo paklaidos pagal jų atsiradimo priežastis yra skirstomos į sistemingąsias ir atsitiktines.

Sistemingosios paklaidos, kartojant pastovaus fizikinio dydžio matavimus nekintančiomis matavimų sąlygomis, nesikeičia arba kinta determinuotai.

Jeigu kartojant matavimus rezultatai gaunami įvairūs ir atskiri rezultatai negali būti prognozuojami, tai reiškia, kad jie gauti veikiant atsitiktinėms paklaidoms.

Taigi matavimo metu gautą atskiro rezultato paklaidą Δ galima išreikšti suma:

$\Delta= \Delta_s+ \Delta_A$

čia Δ_s – matavimo sistemingoji paklaida, Δ_A – matavimo atsitiktinė paklaida.

Sistemingosios paklaidos nusako determinuotą paklaidų dalį. Jos gali būti nekintančios arba kisti determinuotu dėsniu. Pagal atsiradimo priežastis sistemingosios paklaidos klasifikuojamos į keletą grupių: matavimo metodo; matavimo priemonių (matavimo instrumentų, aparatūros), kurios atsiranda dėl matavimo priemonių netobulumo; neteisingo matavimo priemonės; naudojimo ir matuo­tojo paklaidos. Kadangi sistemingosios paklaidos yra dėsningos, tai jas galima sukompensuoti. Dažniausiai sistemingosios paklaidos eliminuojamos, įvedant į matavimo rezultatą pataisas arba pašalinant šių paklaidų atsiradimo priežastis. Tokie rezultatai, kai eliminuojamos sistemingosios paklaidos, vadinami ištaisytaisiais.

Kai sisteminės paklaidos įvertintos, matavimo prietaiso tikslumas žinomas, galima suformuluoti tokias matavimo taisykles: